[CS231n 2016] 5강 Training NN part 1

mini-batch SGD
loop:
1. Sample a batch of data
2. Forward prop it through the graph, get loss
3. Backprop to calculate the gradients
4. Update the parameters using the gradient
Training Neural Networks (a bit of history)
- 1957, Mark 1 Perceptron -> back prop 불가
- 1960, perceptron의 stacking, Adaline/Madaline
1960~1980 신경망의 1번째 암흑기..
- 1986, Rumelhart et al, First time back-propagation became popular
-> 네트워크가 커질 수록 잘 동작이 안됨..
~ 2000 중반, 신경망의 2번째 암흑기
- 2006, Hinton and Salakhutdinov
-> Restricted Boltzman Machine(RBM)을 이용하여 pretraining을 도입
-> 하나로 통합 후 backprop, 그 후 finetuning 사용
=> 제대로 동작하는 첫번째 backprop
황금기(폭발적인 발전)
- 2010, Context-Dependent Pre-trained Deep Neural Networks for Large Vocabulary Speech Recognition
- 2012, Imagenet classification with deep convolutional neural networks
요인, 요소 : weight 초기화 방법 발전, GPU 환경, 데이터 증가
Activation Functions
Sigmoid


- 넓은 범위의 숫자들을 [0,1] 범위의 숫자로 squash해준다.
- 전통적으로 자주 사용해왔지만 더이상 잘 사용하진 않는다.
문제점
- 뉴런이 포화되어(0 또는 1에 가까워짐) gradient를 없애버릴 수 있다. (vanishing gradient)
(x의 값이 꽤 크거나 작은 경우에는 local gradient가 0에 가까워지게 됨 -> 그래프에서 saturated regime인 구역)
- Sigmoid의 결과는 zero-centered가 아니다. -> slow convergence를 가져오게 됨.
(w의 gradient가 항상 all positive이거나 negative이기 때문)
- exp()가 연산적으로 비쌈
tanh(x)

- [-1, 1] 범위로 숫자들을 squash 해준다.
- zero centered 되어 있다.
- 여전히 뉴런이 포화되어(0 또는 1에 가까워짐) gradient를 없애버릴 수 있다. (vanishing gradient)
ReLU


- x가 양수인 지점에서는 포화되지 않음
- 연산적으로 효율적이다.
- sigmoid/tanh에 비해 수렴되는 속도가 6배정도 빠르다.
문제
- zero-centered가 아니다.
- 음수인 경우에 vanishing gradient가 발생
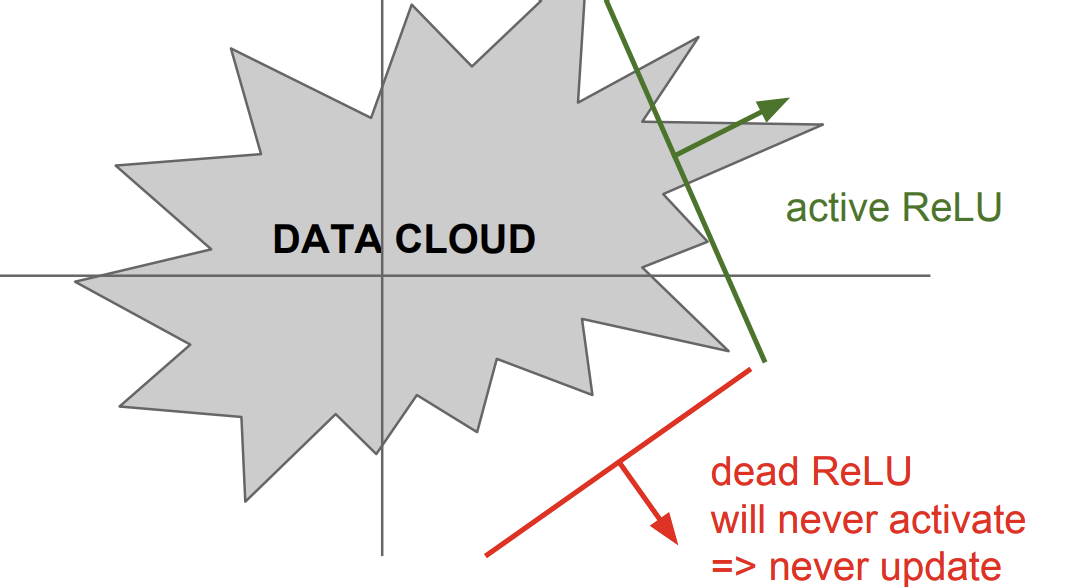
dead ReLU는 learning rate가 너무 크거나, weight 초기화가 운이 나쁘게 잘못되었을 때 발생함.
=> 이를 방지하기 위해 작은 양수 값으로 초기화하는 경우도 있음
Leaky ReLU

- saturate가 일어나지 않음
- 효율적인 연산
- converge가 빠름
- will not 'die' (gradient..)
Parametric Rectifier

Exponential Linear Units(ELU)

- ReLU의 장점을 가지고 있음
- not die
- zero mean outputs에 가까움
- 연산에서 exp()을 가지고 있음
Maxout "Neuron"

- Does not have the basic form of dot product -> nonlinearity
- ReLU와 Leaky ReLU를 일반화
- saturateX, note die
- 2배로 증가하는 연산과 파라미터
결론
- ReLU를 사용, 단 learning rate에 주의
- Leaky ReLU/ Maxout / ELU를 실험적으로 사용
- tanh를 실험적으로 사용하지만 기대X
- sigmoid는 사용X
Data Preprocessing

단, 이미지 데이터에서는 정규화는 진행하지 X
이미지는 기본적으로 [0~255]안에 들어가 있기 때문

=> 사실 이미지에 있어서 둘다 사용은 X
이미지에서는 정규화, PCA, whitening은 흔하게 사용하지 않고, 사실상 zero-centered만 신경 쓰면 된다.
- 이미지의 평균 값을 빼준다. (e.g. AlexNet)
- 채널별 평균 값을 빼준다. (e.g. VGGNet)
Weight Initialization
Q : 만약 W=0으로 초기화 되어 있다면?..
모든 뉴런들이 동일한 연산을 수행하고, back prop을 수행함.
small random numbers


=> 네트워크가 작을 때에는 동작하지만, 커지게 되면 문제가 발생함.
standard variance이 0으로 수렴하게 되고 결과적으로 모든 activation이 0이 되어버림
=> vanishing gradient가 발생
0.01 대신 1을 쓴다면 거의 모든 뉴런들이 saturate 됨. -> Gradient가 0이 되어버림
Xavier initialization
input의 개수가 많으면 weight가 작아짐, 개수가 적으면 weight가 커짐

- 문제 : ReLU를 사용할 때 문제가 생김. (but when using the ReLU nonlinearity it breaks.)
He et al., 2015 (note additional /2)

Batch Normalization
vanishing gradient가 발생하지 않도록 하는 해결방법 중 하나
(activation 함수 변화, 가중치 초기화 방법이 아니라 학습하는 과정 자체를 안정화하는 것을 목표로 함.)
각 layer를 거칠 때마다 normalization을 진행



보통 Fully connected layer와 activation layer 사이에 위치하게 된다.

1. Normalize
2. 정규화 된 것을 조정(r-> 스케일링 B->shift)

장점
- gradient flow를 향상
- 큰 lr도 허용시켜준다.
- 초기화에 대한 강한 의존성을 상쇄시켜준다.
- regularization의 효과가 있음
주의
- training, test 할때 batch normalization을 다르게 해 줘야 한다.
- mean/std를 구할 때 training은 batch를 기준, test는 전체를 기준
Babysitting the learning process
1. 데이터 전처리 (zero-centered)
2. choose the architecture (sanity check)
훈련 전, 데이터 중 일부만 가져와 regularization을 끄고 simple vanilla 'sgd'를 사용해 overfitting이 되는지 확인
(back prop이 잘 작동하고 있다는 뜻)
loss not going down : learning rate too low
loss exploding : learning rate too high
cross validation을 사용해 적절한 learning rate를 알아내야 함.
Hyperparameter Optimization
cross-validation 전략
First stage: only a few epochs to get rough idea of what params work
Second stage: longer running time, finer search
First stageg


-> random search 방법

기본적으로 grid search는 오히려 최적화된 parameter를 찾기 어렵다.
Hyperparameters to play with
- network architecture
- learning rate, its decay schedule, update type
- regularization (L2/Dropout strength)
hyperparameter를 조정한 뒤 loss curve를 관찰해야 한다.

다양한 그래프
- bad 초기화로 다음과 같은 그래프가 나옴.

hyperparameter를 조정한 뒤 accuracy를 관찰해야 한다.

weight updates/ weight magnitudes 를 관찰해야 한다.
