
Data Augmentation
원본의 이미지를 변형하는 과정이 추가되는 방법

- label은 변화 없이 pixel이 변화하게 됨.
- 변형된 data를 훈련 하게 됨
- 매우 폭넓게 사용되고 있음
1. Horizontal flips
이미지를 좌우반전 시켜 변형해주는 방법
- mirror 이미지
2. Random crops / scales
이미지를 랜덤으로 작은 부분으로 잘라내어 사용하는 방법
이미지 전체가 아니라 부분에 대한 학습이 이뤄지기 때문에 test 시에도 이미지 전체가 아닌 crop을 이용해 test를 진행하게 된다.

3. Color jitter
단순한 방법 : random으로 jitter

복잡한 방법 :
1) training set의 [R, G, B]에 PCA를 적용한다.
2) 주성분 방향의 color offset를 샘플링한다.
3) training image의 모든 픽셀에 offset을 더해준다.
4. 그 외의 방법 ...
- translation
- rotation
- stretching
- shearing
- lens distortions ...
- etc
A general theme :
1. Training : 랜덤한 노이즈를 적용
2. Testing : 노이즈들을 평균화하는 작용
Data Augmentation은 dropout, dropconnect 과 비슷하다고 볼 수 있다.
따라서 Data Augmentation은 구현하기가 간단하고, 특히 작은 dataset에서 유용하다.
또한 noise와 marginalization을 적용시키는 간단한 framework가 된다.
Transfer Learning
잘못된 믿음 -> "CNN을 사용할려면 많은 데이터가 필요하다."
Transfer Learning with CNNs
데이터 셋이 작은 경우에는 미리 학습된 모델의 앞단의 부분을 freeze(파라미터 고정)하고 뒷부분으로 데이터셋으로 학습하는 방법을 적용할 수 있다. 데이터가 medium size인 경우에는 조금 더 많은 부분을 설정해서 학습 시킬 수 있다.

일반적으로는 이미 학습된 모델을 가져와 학습하는 것이 더 성능이 좋다...
-> 왜그럴까?...
앞단에서는 굉장히 low level feature(ex. edge, gabor filter...)를 학습하기 때문에 어떤 이미지를 학습하더라도 적용이 될 수 있다. 따라서 위와 같은 결과가 나오는 것!...
데이터의 유사성과 데이터의 수에 따른 대처 방법

사실 CNN에서의 Transfer Learning은 보편적이다...
ex) Object Detection(Faster R-CNN), Image Captioning ...
All About Convolutions
Part 1 : How to stack them
- small filter의 power
예를 들어 3x3 conv layer를 3개 쌓는다면 이는 하나의 7x7 convolution과 동일한 효과를 낸다.
둘의 weight의 개수를 비교해보면, Cx(7x7xC) = 49C^2 , 3xCx(3x3xC)=27C^2 이다.
결국 3개의 3x3 conv layer가 parameter의 수도 적고 더 nonlinearity를 가지기 때문에 좋다고 볼 수 있다.
또한 곱셈 연산의 수를 비교해보면
(H x W x C) x (7 x 7 x C) = 49 HWC^2, 3 x (H x W x C) x (3 x 3 x C) = 27 HWC^2
마찬가지로 3개의 3x3 conv layer가 곱셈연산의 수도 더 적다.
그렇다면 1x1 filter는?...

이를 3x3 filter와 비교해보면 bottleneck conv가 더 nonlinear하고 더 적은 parameter, 더 적은 연산이 들게 된다.

하지만, 아직 3x3 filter를 사용하고 있다. 다른 방법?...

위와 같은 filter 들을 많은 곳에서 사용하고 있다.

Recap
- 큰 conv 대신 3x3의 conv를 사용하는 것이 효율적이다.
- 1x1 "bottleneck" conv도 효율적인 방법이다.
- nxn filterfmf 1xn, nx1로 나누어 사용할 수 있다.
- 위의 모든 방법들은 더 적은 parameter를 가지고, 연산량이 적으며 더 nonlenear하다.
Part 2 : How to compute them
Implementing Convolutions : im2col
대부분의 플랫폼에서는 matrix multiplication을 잘 최적화 해놓음.
그렇다면 convolution 연산을 matrix multiplication연산으로 표현 할 수 있을까?
=> im2col 사용!
Feature map : HxWxC
Con weights : D filters, each KxKxC 라고 하면, 먼저 K^2C 의 column vecter를 N번(receptive field의 개수) 만큼 반복한 형태를 만들어준다.


filter를 K^2C의 row vector 로 reshape해서 Dx(K^2C) matrix를 만들어준다. 이를 matrix multiply를 해주면
DxN 결과가 나온다.

Implementing convolutions: FFT
f와 g를 convolution 연산한 것은 Fourier Trasform의 element product와 동일하다.
Fast Fourier Transform을 이용하면, 우리는 N차원의 벡터의 Discrete Fourier transform를 O(N log N)으로 계산할 수 있다.
1. Compute FFT of weights: F(W)
2. Compute FFT of image: F(X)
3. Compute elementwise product: F(W) ○ F(X)
4. Compute inverse FFT: Y = F-1(F(W) ○ F(X))
Implementing convolutions: Fast Algorithms
Naive matrix multiplication: Computing product of two N x N matrices takes O(N3 ) operations
Strassen’s Algorithm: Use clever arithmetic to reduce complexity to O(Nlog2(7)) ~ O(N2.81)
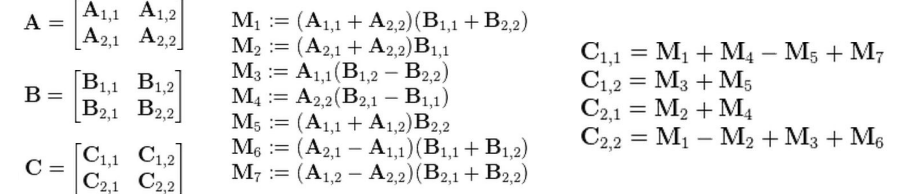
Recap
im2col : 구현하기 쉽지만 memory overhead가 발생할 수 있음.
FFT : 작은 커널에서는 성능향상을 가져올 수 있음.
Fast Algorithms : 유망한 분야이지만, 아직 널리 사용되지는 않음.
Implementation Details
CPU... GPU...
CPU : Few, fast cores (1 - 16) Good at sequential processing
GPU : Many, slower cores (thousands) Originally for graphics Good at parallel computation
GPU - CPU communication is a bottleneck.
=> CPU data prefetch+augment thread running while GPU performs forward/backward pass
CPU - disk bottleneck Hard disk is slow to read from
=> Pre-processed images stored contiguously in files, read as raw byte stream from SSD disk
Floating Point Precision
소수점의 정확도
보통은 64 bit "double" precision이 기본값이다.
하지만 CNN에서는 32bit "single" precision로 빠른 연산을 수행한다.
또한 stochastic rounding이라는 방법을 사용한 16-bit fixed point로 학습한 것이 높은 성능을 보임

'컴퓨터비전' 카테고리의 다른 글
| [CS231n 2016] 13강 Segmentation and Attention (0) | 2022.07.26 |
|---|---|
| [CS231n 2016] 10강 Recurrent Neural Networks (0) | 2022.07.18 |
| [CS231n 2016] 9강 Understanding and Visualizing Convolutional Neural Networks (0) | 2022.07.15 |
| [CS231n 2016] 8강 Spatial Localization and Detection (0) | 2022.07.14 |
| [CS231n 2016] 7강 Convolutional Neural Network (0) | 2022.07.11 |